ആരം

ഇംഗ്ലീഷ് വിലാസം

https://ml.wikipedia.org/wiki/Radius

R- ആരവും, O- കേന്ദ്രബിന്ദുവും ആയിട്ടുള്ള ഒരു വൃത്തം

ജ്യാമിതിയിൽ, ഒരു വൃത്തം അല്ലെങ്കിൽ ഗോളത്തിന്റെ കേന്ദ്രത്തിൽ നിന്നും അതിന്റെ പരിധിവരെയുള്ള ദൂരമാണ് ആരം എന്നറിയപ്പെടുന്നത്. കിരണം എന്നും രഥചക്രത്തിന്റെ ആരക്കാൽ എന്നും ഒക്കെ അർഥമുള്ള ലാറ്റിൻ വാക്ക് റേഡിയസിൽ (radius) നിന്നാണ് ആരത്തിൻ്റെ ഇംഗ്ലീഷ് വാക്ക് റേഡിയസ് ഉദ്ഭവിച്ചത്. ആരത്തിന്റെ സാധാരണ ചുരുക്കെഴുത്തും ഗണിതശാസ്ത്ര ചര നാമവും r ആണ്. ആരത്തിന്റെ ഇരട്ടിയാണ് വ്യാസം (d).

$d\doteq 2r\quad \Rightarrow \quad r={\frac {d}{2}}.$

ചുറ്റളവ് C ഉള്ള വൃത്തത്തിന്റെ ആരം കണക്കാക്കുന്ന സൂത്രവാക്യമാണ്

$r={\frac {C}{2\pi }}.$

സൂത്രവാക്യങ്ങൾ

പല ജ്യാമിതീയ രൂപങ്ങളിലും, ആരം അതിന്റെ മറ്റ് അളവുകളുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു.

വൃത്തം

വിസ്തീർണ്ണം A ഉള്ള ഒരു വൃത്തത്തിന്റെ ആരം കണക്കാക്കുന്ന സൂത്രവാക്യമാണ്.

$r={\sqrt {\frac {A}{\pi }}}.$

നേർരേഖയിലല്ലാത്ത P₁, P₂, P₃ എന്നീ മൂന്ന് ബിന്ദുക്കളിലൂടെ കടന്നുപോകുന്ന വൃത്തത്തിന്റെ ആരമാണ്:

$r={\frac {|{\vec {OP_{1}}}-{\vec {OP_{3}}}|}{2\sin \theta }},$

ഇതിൽ θ എന്നത് ∠P₁P₂P₃ കോൺ ആണ്. ലോ ഓഫ് സൈൻ ഉപയോഗിക്കുന്ന സൂത്രവാക്യമാണ് ഇത്. മൂന്ന് പോയിന്റുകൾക്ക് പകരം അവയുടെ കോർഡിനേറ്റുകൾ (x₁,y₁), (x₂,y₂), (x₃,y₃) എന്നിങ്ങനെ നൽകിയാൽ, താഴെപ്പറയുന്ന സൂത്രവാക്യ പ്രകാരം ആരം കണക്കാക്കാം.

$r={\frac {\sqrt {[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}][(x_{2}-x_{3})^{2}+(y_{2}-y_{3})^{2}][(x_{3}-x_{1})^{2}+(y_{3}-y_{1})^{2}]}}{2|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{2}y_{1}-x_{3}y_{2}|}}.$

ക്രമീകൃത ബഹുഭുജങ്ങൾ

n	Rn
3	0.577350 ...
4	0.707106 ...
5	0.850650 ...
6	1.0
7	1.152382 ...
8	1.306562 ...
9	1.461902 ...
10	1.618033 ...

ഉദാഹരണത്തിന് ഒരു ചതുരം ( n = 4)

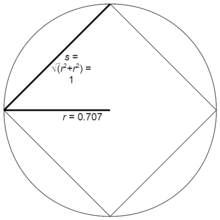
s നീളവും n എണ്ണം വശങ്ങളും ഉള്ള ഒരു റഗുലർ പോളിഗണിലെ ആരം r കണക്കാക്കുന്ന സൂത്രവാക്യമാണ് r = R_n s. ഇതിൽ R_n കണക്കാക്കാൻ ഉപയോഗിക്കുന്ന സൂത്രവാക്യമാണ് $R_{n}=1\left/\left(2\sin {\frac {\pi }{n}}\right)\right..$ s = 1 ആണെങ്കിൽ, ഈ മൂല്യങ്ങൾ അനുബന്ധ റഗുലർ പോളിഗണുകളുടെ ആരം കൂടിയാണ്

ഹൈപ്പർക്യൂബുകൾ

s വശമുള്ള ഒരു d-ഡൈമൻഷണൽ ഹൈപ്പർക്യൂബിന്റെ ആരം ആണ്:

$r={\frac {s}{2}}{\sqrt {d}}.$