സമപാർശ്വ ത്രികോണം
| സമപാർശ്വ ത്രികോണം | |
|---|---|
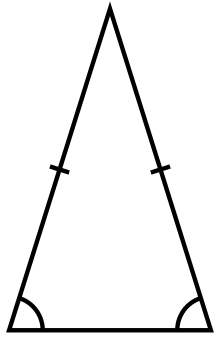 Isosceles triangle with vertical axis of symmetry | |
| തരം | triangle |
| വക്കുകളും ശീർഷങ്ങളും | 3 |
| Schläfli symbol | ( ) ∨ { } |
| Symmetry group | Dih2, [ ], (*), order 2 |
| Dual polygon | Self-dual |
| സവിശേഷതകൾ | convex, cyclic |
ജ്യാമിതിയിൽ രണ്ടു വശങ്ങൾ തുല്യമായ ത്രികോണത്തെ സമപാർശ്വത്രികോണം എന്നു പറയുന്നു.ചിലപ്പോൾ രണ്ടു വശങ്ങൾ മാത്രം തുല്യംഎന്നും ചിലപ്പോൾ ചുരുങ്ങിയത് രണ്ടു വശമെങ്കിലും തുല്യമായതെന്നും പറയാറുണ്ട്. രണ്ടാമതു പറഞ്ഞതിൽ സമഭുജ ത്രികോണവും പെടും. സമപാർശ്വ ത്രികോണ നിയമ പ്രകാരം, സമമായ വശങ്ങളുടെ എതിരെയുള്ള കോണുകളും സമമായിരിക്കും. അതേസമയം മൂന്നാമത്തെ വശത്തിന്റെ അളവ് വ്യത്യസ്തമാണെങ്കിൽ അതിന് എതിരെയുള്ള കോണും വ്യ്ത്യസ്തമായിരിക്കും.

രണ്ടു വശങ്ങളുടെ നീളങ്ങൾ തുല്യമായ ത്രികോണമാണ് സമപാർശ്വ ത്രികോണം (isosceles triangle). തുല്യമായ വശങ്ങൾക്ക് എതിരെയുള്ള കോണുകളും തുല്യമായിരിക്കും. ആ കോണുകളെ പാദകോണുകൾ (base angles) എന്നു വിളിക്കുന്നു.
സമപാർശ ത്രികോണങ്ങളിൽ രൺടു വശങ്ങൾ തുല്യമായിരിക്കും. തുല്യ മായ പാർസ്വങ്ങളെ വശങ്ങൾ എന്നും മൂന്നാമത്ത് വ്ശത്തെ പാദം എന്നും പറയും. തുല്യവശങ്ങൾ ഉൽക്കൊണ്ട കോണിനെ ശീർഷകോൺ എന്ന് പറയുന്നു.പാദം ഒരു വശമായുള്ള കോണിനെ പാദകോണുകൾ എന്നും പറയും. യൂക്ലിഡ് രണ്ടു വശങ്ങൾ തുല്യമായ ത്രികോണത്തെ സമപാർശ്വ ത്രികോണമെന്ന് നിർവചിച്ചിട്ടുണ്ട്.[1]എന്നാൽ ആധുനിക കാലത്ത് ചുരുങ്ങിയത്ത് രണ്ടൂ വശങ്ങൾ തുല്യമായത് എന്നു നിർവചിച്ച്പ്പോൾ പ്രത്യേക സംഗതിയായി സമഭുജ തികോണങ്ങളേയും ഉൾപ്പെടുത്തിയിട്ടുണ്ട്. [2] സമഭുജ ത്രികോണത്തിൽ മൂന്നു വശങ്ങളും തുല്യമായതുകൊണ്ട് ഏതുവശത്തെ വേണമെങ്കിലും പാദമായി കണക്കാക്കാം.
സമാനത
[തിരുത്തുക]രണ്ടു വശങ്ങൾ മാത്രം തുല്യമായ ത്രികോണത്തിന്റെ സമാന അക്ഷം ശീർഷത്തിലൂടേയും പാദത്തിന്റെ മദ്ധ്യബിന്ദുവിലൂടേയും കടന്നു പോകുന്നു.
സമാന അക്ഷം, (1) ശീർഷകോണിന്റെ സമഭാജി, (2) പാദത്തിലേക്കു വരക്കുന്ന മാധ്യമം(Median ), (3) ശീഷത്തിലേക്കുള്ള ഉന്നതി, പാദത്തിന്റെ ലംബ സഭാജി എന്നിവയുമായി ഏകീഭവിക്കുന്നു. [3]
ന്യൂന, മട്ട, ബൃഹദ് കോണുകൾ
[തിരുത്തുക][[File:45-45-triangle.svg|thumb|കമപാർശ്വ മട്ടത്രികോണം സമപാർശ്വ ത്രികോണം ശീർഷകോണിനെ അടിസ്ഥാനമാക്കി ന്യൂന, മട്ട, ബൃഹദ് ത്രിണമാകും. യൂക്ലീഡിയൻ ജ്യാമിതി പ്രകാരം ത്രികോണത്തിനെ പാദകോണുകൾ മട്ടക്കോണുകളൊ ബൃഹദ് കോണുകളൊ ആകാൻ പറ്റില്ല, കാരണം ത്രികോണത്തിന്റെ കോണുകളുടെ തുക 180° ആയിരിക്കും. സമപാർശ്വത്രികോണത്തിന്റെ ശീർഷ കോണിനെ അടിസ്ഥാനമാക്കിയാണ് അത് ന്യൂന, മട്ട, ബൃഹദ് സമപാർശ്വത്രികോണമെന്ന് കണക്കാക്കുന്നത്..
== സൂത്രവാക്യം == a സമപാർശ്വങ്ങളും b പാദവുമായുള്ള സമപാർശ്വത്രികോണത്തിന്റെ സാമാന്യ ത്രികോണ സൂത്രവാക്യം(1) ശീർഷ കോണിന്റെ സമഭാജി (2)പാദത്തിലേക്കുള്ള മാധ്യമം (3)പാദത്തിലേക്കുള്ള ഉന്നതിപാദത്തിന്റെ ലംബസമഭാജി എന്നിവയ്ക്കുള്ള സാമാന്യ ത്രികോണ സൂത്രവാക്യം For any isosceles triangle with area T വിസ്തീർണ്ണവും p ചുറ്റളവും ഉള്ള സമപാർശ്വത്രികോണത്തിൽ [4]:Eq.(1)
വിസ്തീർണ്ണം
[തിരുത്തുക]The area of an isosceles triangle can be derived using the പൈതഗ്രസ് തത്ത്വം കൊണ്ടാണ് സമപാർശ്വ ത്രികോണത്തിന്റെ വിസ്തീർണ്ണം കണക്കാക്കുന്നത് ,: പാദത്തിന്റെ പകുതിയുടെ വർഗ്ഗത്തിന്റേയും ഉന്നതി യുടെ വർഗ്ഗത്തിൻടേയും തുക ഒരു വശത്തിന്റെ :
വർഗ്ഗത്തിനു തുല്യമായിരിക്കും.
- ,
- .
ഉന്നതിയ്ക്ക് പകരം വച്ച്, സൂത്രവാക്യം നോക്കാം,
- .
ഹെറോൺസ് ഫോർമുല ഉപയോഗിച്ച് സമപാർശ്വ ത്രികോണത്തിന്റെ കാര്യത്തിൽ സംഗ്രഹിക്കുന്നു.
ഒരു സമശീർഷ ത്രികോണത്തിന്റെ ശീർഷ കോൺ യും വശങ്ങൾ യും ആയാൽ വിസ്തീർണ്ണം,
- .
ത്രികോണത്തിന്റെ പാദത്തിൽ നിന്ന് വരയ്ക്കുന്ന ലംബം, ശീർഷ കോണിനെ ഭാഗിച്ച് രണ്ട് മട്ടത്രികോണങ്ങൾ ഉണ്ടാക്കും.
trigonometric identity ഉപയോഗിച്ച് , we get ,
അവലംബം
[തിരുത്തുക]- ↑ Heath 1956, p. 187, Definition 20
- ↑ Stahl 2003, p. 37
- ↑ Ostermann & Wanner 2012, p. 55, Exercise 7
- ↑ George Baloglou and Michel Helfgott. "Angles, area, and perimeter caught in a cubic", Forum Geometricorum 8, 2008, 13-25. http://forumgeom.fau.edu/FG2008volume8/FG200803.pdf Archived 2022-06-23 at the Wayback Machine
*Heath, Thomas L. (1956), The Thirteen Books of Euclid's Elements, vol. 1 (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.), New York: Dover Publications, ISBN 0-486-60088-2
- Jacobs, Harold R. (1974), Geometry, W. H. Freeman and Co., ISBN 0-7167-0456-0
- Ostermann, Alexander; Wanner, Gerhard (2012), Geometry by Its History, Springer, ISBN 978-3-642-29162-3
- Stahl, Saul (2003), Geometry from Euclid to Knots, Prentice-Hall, ISBN 0-13-032927-4
- Venema, Gerard A. (2006), Foundations of Geometry, Prentice-Hall, ISBN 0-13-143700-3














